图像纹理特征提取|灰度共生矩阵

数字图像处理的拓展内容，上课时被分配了“图像检索及 AI 应用”，想搞个小实践水水念 PPT 的时间，就稍微研究下图像纹理特征分析，也顺带写篇博客。

图像检索发展

在 Web2.0 时代，互联网中的信息量爆炸性增长，其中自然包含了很多图片。在 Twitter、FaceBook 等各种社交媒体平台，每月用户上传的图片数量都在 10 亿上下，而以淘宝、亚马逊为代表的电子商务平台，其后台存储的图片数量更是以百亿记。面对如此浩瀚且包含了丰富视觉信息的图片，如何从中精准快速地检索出我们想要的图片，已经成为了多媒体信息检索技术研究的热点。

基于文本的图像检索技术 TBIR

按发展顺序，可先后分为基于文本的图像检索技术（TBIR, Text Based Image Retrieval）和基于内容的图像检索技术（CBIR, Content Based Image Retrieval），前者可以理解为人工/半人工给图片打 tag，然后检索时根据 tag 匹配度检索图片，后者则是正经的使用计算机通过公式化的流程分析图片特征，然后实现以图搜图。

先说 TBIR，这种技术好用吗？确实好用，因为实现难度不高，甚至你自己建立个数据库，给自己收藏的图片打 tag，然写个根据 tag 的搜索功能，这就算是一种 TBIR 的实现。而且因为是通过人工的方式给图像信息打 tag，而用户也是人，这样检索图像的准确率比较高。

但从上述的简单流程就能看出，TBIR 也有一些明显的缺陷：给图片标注文本信息需要人工的介入，如果图像数据很庞大，就会耗费大量人力物力，这使得其无法被用于大规模的图像数据；同时也是因为人工的介入，导致标注信息时难免混入一些标注者的主观考量，同一张图片你很难让两个人给出完全一致的 tag 列表，这就会导致检索时的不准确。再另一方面，很多用户本身也没法做到精确描述自己需要的图片信息，比如下面这张图：

你可能很喜欢这种风格，然后你打开了 Pinterest，接下来应该搜索什么关键词来描述这种风格呢？经验丰富的标注者可以使用 LowPoly 精准描述这种风格，但多数用户不能，这问题不是 TBIR 能解决的，毕竟连用户都不知道要搜什么，检索能力再强也没用。

基于内容的图像检索技术 CBIR

所以，在 1992 年，美国国家科学基金会就图像数据库管理系统新发展方向达成一致共识，表示索引图像信息的最有效方式应该是基于图像内容自身的。自此，基于内容的图像检索技术便逐步建立起来，并在近十多年里得到了迅速的发展。

典型的 CBIR 框架如下，大致可总结为三个阶段：

1. 特征提取：计算机分析图像数据库中的每张图片，提取出颜色、纹理、形状等低层次视觉特征，并将这些特征转化为特征向量存储在图像特征库中。
2. 查询处理：当用户提交一张查询图像时，系统会用相同的方法提取其特征。
3. 相似性度量与排序输出：系统将查询图像的特征向量与特征库中的向量进行比较，根据相似性度量准则计算相似度，并将结果按相似度高低排序输出。

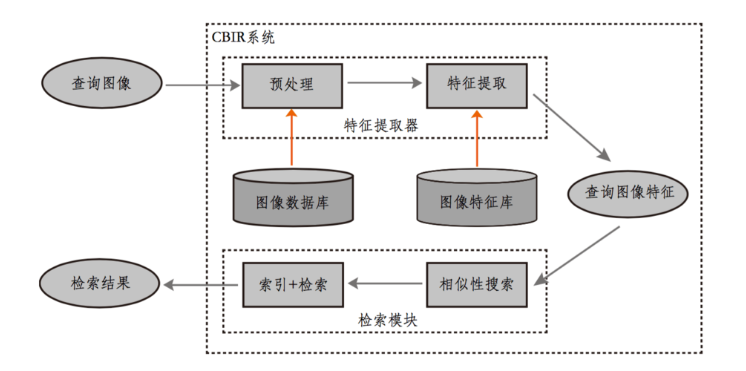
CBIR 将标注图片、分析图片、检索图片的工作全部交给计算机，客服了 TBIR 的不足，极大地提高了检索效率以及可使用图像检索技术的规模。但也带来了一个问题：计算机不是人类，它很难理解高层语义，所以其图像特征的描述与人类存在语义鸿沟。

这“高层语义”指的是人类对图像内容的抽象理解，比如识别图像中的场景或情感。这些含义通常超出了简单的视觉特征所能表达的范围，你可以使用“可爱”这种描述搜索出毛茸茸的小猫小狗，计算机很难办到，因为计算机无法直接理解“可爱”是什么，语义鸿沟是无法消除的，它只能通过一些额外的手段来弥补这种鸿沟。比如在实现图像检索时就预先告知计算机，“可爱”这种特征可以拆解为“多毛”、“眼睛在面部占比大”、“头身比低”等一系列特征，然后再将这些特征一步步分解，直到转化为计算机可以理解的图像视觉特征，比如纹理、颜色、形状等。

但经过这一道道的转化，图像检索的准确率就会无可避免的下降，然后就需要再通过其他额外手段弥补这种缺陷。这就导致了 CBIR 虽然在很大程度解放了人力，但实现起来比较困难。

TBIR 和 CBIR 在现代都得到了广泛应用。分别别举一个贴近生活的案例：常见的图片素材库，比如 Pinterest 和 花瓣网，都主要依靠 TBIR 技术；电子商务方面比如淘宝的拍立淘，就是主要基于 CBIR 技术。

然后呢，随着 AI 技术大力发展，人们发现可以和图像检索技术结合使用，现代图像检索技术与 AI 的结合主要涉及到深度学习等新技术的研究和应用。深度学习可以自动学习和提取图像中的特征，处理更复杂的场景和任务。例如，深度神经网络能够自动提取图像特征进行分类，生成对抗网络（GAN）可以生成相似图片扩展数据集，自编码器可用于降噪和去模糊等。

图像通用视觉特征

图像特征的提取与表达是 CBIR 的基础。广义上讲，图像的特征包括基于文本的特征和视觉特征，前者在数据库系统和信息检索领域已有深入研究，这里只介绍后者。

而视觉特征又可以分为两类：通用视觉特征和领域相关视觉特征。通用视觉特征就是我们肉眼所能看到的基本信息，适用于所有类型的图像；而领域相关视觉特征则依赖于特定领域的知识，如面部或指纹特征。不同的表达方法可以从不同角度描述一个特征，并没有所谓的“最佳”表达方式。

通用视觉特征包括我们最常用的三种对图像的描述方式：色彩、纹理与形状。

颜色特征

颜色特征是在图像检索中应用最为广泛的视觉特征，主要原因在于颜色往往和图像中所包含的 物体或场景十分相关。此外，与其他的视觉特征相比，颜色特征对图像本身的尺寸、方向、视角的依赖性较小，从而具有较高的鲁棒性。

纹理特征

纹理特征是一种不依赖于颜色或亮度的反映图像中同质现象的视觉特征。它是所有物体表面共有的内在特性，例如云彩、树木、砖、织物等都有各自的纹理特征。纹理特征包含了物体表面结构组织排列的重要信息以及它们与周围环境的联系。正因为如此，纹理特征在 CBIR 中得到了广泛的应用。纹理特征具有四大特点：

• 局部序列性重复
• 非随机排列
• 区域内均匀统一
• 旋转不变性

它通过像素及其周围空间邻域的灰度分布来表现局部纹理信息，并通过不同程度上的重复性展现全局纹理信息。纹理特征在模式匹配中具有优势，因为它是基于区域的统计计算，不容易受局部偏差影响。在检索纹理图像时，纹理特征可以有效区分粗细、疏密等差异较大的纹理，但在纹理之间差异不明显时，可能无法准确反映人眼的视觉感知。一些虚假纹理，如水中倒影或金属面反射造成的影响，可能会误导检索结果。

形状特征

物体和区域的形状是图像表达和图像检索中的另一重要的特征。但不同于颜色或纹理等底层特 征，形状特征的表达必须以对图像中物体或区域的划分为基础。由于当前的技术无法做到准确而鲁棒的自动图像分割，图像检索中的形状特征只能用于某些特殊应用，在这些应用中图像包含的物体 或区域可以直接获得。另一方面，由于人们对物体形状的变换、旋转和缩放主观上不太敏感，合适的形状特征必须满足对变换、旋转和缩放无关，这对形状相似度的计算也带来了难度。

纹理特征提取：灰度共生矩阵

灰度共生矩阵（Gray-level Co-occurrence Matrix, GLCM）是计算机视觉领域常用的分析图像纹理特征的一种统计方法。

GLCM 本质上是一种矩阵，但我们通常会使用 GLCM 指代基于这种矩阵的分析方法。

GLCM 的概念在 1973 年由 Haralick 等人首次提出，目的是描述图像的纹理特征。因为纹理是由灰度分布在空间位置上反复出现而形成的，所以在图像空间中相隔某距离的两像素之间会存在一定的灰度关系，即图像中灰度的空间相关特性。GLCM 就是用来描述这种空间相关性的，这也是“共生”这个词的意义。所以说 GLCM 描述的从来不是单个像素，而是成对的像素之间的关系。与之相对的，灰度直方图（Grayscale Image Histogram，GIH）则可以看做是对单个像素的统计与描述，并不涉及灰度间的关联关系。

img = imread('test.jpg');

grayImg = rgb2gray(img);

glcm = graycomatrix(grayImg);

figure;

subplot(1,2,1), imshow(img), title('Original Image');
subplot(1,2,2), imshow(glcm,[]), title('GLCM');

可以使用以上 MATLAB 代码，获取一张普通的 jpg 图片的 GLCM 并进行对比：

计算方法

1. 确定量化级数：根据图像的灰度级别，创建一个方阵，通常是 256x256；
2. 定义邻域关系：选择像素对的方向（水平、垂直、对角等）和距离（步长）；
3. 统计频次：遍历图像，对于每个像素对(i,j)，如果它们的灰度级满足所定义的邻域关系，则在 GLCM 矩阵中相应位置(i,j)的值加一；
4. 计算概率：将GLCM矩阵中的每个元素除以总次数，得到每种关联模式出现的概率。

Ok，明白了计算方法，我们就可以尝试自己写个 demo 出来试试成果哩。MatLab 我用得实在是不熟（平成确实没有使用场景），所以接下来的代码是使用 python 完成的。思路也很清晰，使用 PIL 读取图像并转化为灰度图像，然后使用 numpy 计算并创建对应的灰度共生矩阵图像，最后使用 matplotlib 库对原图以及灰度共生矩阵图像进行一个展示：

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt

# 读取图片并转换为灰度图像
def read_image(file_name):
    return np.array(Image.open(file_name).convert('L'))

# 创建灰度共生矩阵
def create_glcm(image, d=1, theta=0):
    max_gray_level = 256
    glcm = np.zeros((max_gray_level, max_gray_level))
    rows, cols = image.shape

    for i in range(rows):
        for j in range(cols - d):
            rows_value = image[i][j]
            cols_value = image[i][j + d] if theta == 0 else image[i + d][j]
            glcm[rows_value][cols_value] += 1

    return glcm

def main():
    image_a = read_image('a.jpg')
    glcm_a = create_glcm(image_a)

    plt.figure(figsize=(10, 5))

    plt.subplot(1, 2, 1)
    plt.imshow(image_a, cmap='gray')
    plt.title('Original Image')
    plt.axis('off')

    plt.subplot(1, 2, 2)
    plt.imshow(glcm_a, cmap='gray')
    plt.title('GLCM of Image')
    plt.axis('off')

    plt.show()

if __name__ == "__main__":
    main()

特征

前面说了，GLCM 严格说是一种用于描述图像纹理特征的二维矩阵。这个矩阵每行或每列代表不同灰度级别的出现关系，对角线表示相邻像素灰度一致性。对每行进行累加可得到一个 256 维向量，表示原图中每个灰度级别像素的出现次数，类似灰度直方图。全元素求和等于总像素个数减去步长乘以跳跃次数。其不一定对称，因为 (1,3) 和 (3,1) 表示不同灰度关系。这种特殊的矩阵具有四个特性，分别是：

1. 对比度：用于度量矩阵值的分布和局部变化，反应图像的清晰度和纹理的沟纹深浅。对比度越大，影像越清晰。计算公式如下，其中 i、j 为共生矩阵中的坐标索引，P(i,j) 为该位置的灰度值（对于共生矩阵来说就是某种灰度关联关系出现的次数）：

   [Con = \sum_{i}^{} \sum_{j}^{} (i-j)^{2}P(i,j)]

2. 能量：灰度共生矩阵元素值的平方和，称其为能量，也叫第二角力矩（Angular Second Moment, ASM）。反应了图像灰度分布均匀程度和纹理粗细度。如果其较大，则表明图像中存在一种较为均一和规则变化的纹理模式。计算公式如下：

   [Asm = \sum_{i}^{} \sum_{j}^{} P(i,j)^{2}]

3. 熵：在灰度共生矩阵中表示图像的信息量。当共生矩阵中元素分布较为分散时，熵较大。它表示了图像中纹理的非均匀程度或者复杂程度。计算公式如下：

   [Ent = \sum_{i}^{} \sum_{j}^{} P(i,j)logP(i,j)]

4. 相关度：度量灰度共生矩阵元素在行或列方向上的相似程度（Inverse Different Moment）。其值反应了图像中局部灰度相关性。当矩阵元素均匀相等时，相关度较大，反之较小。计算公式如下：

   [IDM = \sum_{i}^{} \sum_{j}^{} \frac{P(i,j)}{1+(i-j)^{2}}]

虽然我们掌握了四种特性值的计算方法，可以用文本数值对图像的纹理特征进行表示了，但还是有不方便的地方，将两组图像的纹理特征进行对比时，如果两项特性值高、两项特性值低该怎么办？这就需要归一化处理。对 GLCM 进行归一化处理的主要目的是消除图像大小、对比度等因素对特征计算的影响，从而使得特征更具有普适性和可比性。这样做的好处包括：

GLCM 的归一化主要包括两种常见的方法：

• 将 GLCM 矩阵中的元素值除以 GLCM 矩阵中所有元素值的和，使得归一化后的 GLCM 矩阵中所有元素之和为1
• 将 GLCM 矩阵中的元素值除以 GLCM 矩阵中元素值的平方和的平方根，使得归一化后的 GLCM 矩阵中元素值的平方和为1。

进行归一化处理后得到的数值一般被称为 规范化纹理特征，我们可以使用该值对图像之间的纹理特征进行一个就更加具象的对比。

进一步实践

掌握了以上内容，现在我们可以做一个更加贴近现实的实践了。我准备了三张图片，有两张是动物的皮毛，还有一张是爬行动物的鳞甲图（下面这张图是实验结果的一部分，三张图片原图是彩图，不过对实验没什么影响）：

使用 Python 分别计算三张图片的灰度共生矩阵，然后计算四项特征值，再进行归一化处理，最后根据规范化纹理特征判断哪两张图像的纹理特征更接近。因为代码里很多内容是在调用函数、输出结果以及展示图片，所以不全贴出来，只展示部分核心代码，也就是做计算提取图像纹理特征那块，完整代码上传到了我的一个存储学校作业的 GitHub 仓库中，位于“数字图像处理”目录下，也包括了三张示范图片，可以自行前往查看。点击此 链接 前往。

以下为核心函数代码：

# 读取图片并转换为灰度图像
def read_image(file_name):
    return np.array(Image.open(file_name).convert('L'))

# 创建灰度共生矩阵
def create_glcm(image, d=1, theta=0):
    max_gray_level = 256
    glcm = np.zeros((max_gray_level, max_gray_level))
    rows, cols = image.shape

    for i in range(rows):
        for j in range(cols - d):
            rows_value = image[i][j]
            cols_value = image[i][j + d] if theta == 0 else image[i + d][j]
            glcm[rows_value][cols_value] += 1

    return glcm

# 计算特征值
def calculate_features(glcm):
    contrast = np.sum(np.square(np.arange(glcm.shape[0]) - np.arange(glcm.shape[1])) * glcm)
    energy = np.sum(np.square(glcm))
    entropy = -np.sum(glcm * np.ma.log(glcm).filled(0))
    inverse_diff_moment = np.sum(glcm / (1 + np.square(np.arange(glcm.shape[0]) - np.arange(glcm.shape[1]))))

    return contrast, energy, entropy, inverse_diff_moment

# 归一化处理
def normalize_features(features):
    normalized_features = (features - np.mean(features)) / np.std(features)
    return normalized_features

运行结果，轻松得出 a 与 b 更加相似的结论：

阅读文档

• https://github.com/scikit-image/skimage-tutorials

• https://leovan.me/cn/2022/01/content-based-image-retrieval/

• https://www.cs.cmu.edu/~juny/Prof/papers/Part2-CBIR.pdf

• 特征提取——纹理特征-腾讯云开发者社区-腾讯云 (tencent.com)

• GLCM 灰度共生矩阵与 Haralick 特征-腾讯云开发者社区-腾讯云 (tencent.com)

• 纹理特征提取方法：LBP, 灰度共生矩阵-腾讯云开发者社区-腾讯云 (tencent.com)

• http://zhaoxuhui.top/blog/2022/03/15/gray-level-co-occurence-matrix.html